Welcome to Neal´s Mandelbrot Set and Julia Set Page!

This modest page is devoted to explaining two wonderful, related mathematical notions: the Mandelbrot Set and Julia sets.  If you have the Java 2 Plug-in, you can run a really fancy applet that allows you to explore these sets interactively.

• What is the Mandelbrot Set?
• Mandelbrot Set Pictures
• What is a Julia set?
• Julia Set Pictures
• Image Gallery
• Links to Other Mandelbrot/Julia Pages
• JManEx - Mandelbrot/Julia Applet

What is the Mandelbrot Set?

The Mandelbrot Set is a mathematical object in the complex plane -- any complex number is either a member or not a member of the Mandelbrot Set.  The set is named after Benoit Mandelbrot, a mathematician who studied complexity and information theory, and the man who coined the term "fractal". The entire set is shown, in a bird's-eye view, in the image on the right.  The black portion are points that are members of the set.

Review of Complex Numbers

First, let's review the idea of a complex number. A complex number has a real part and an imaginary part. We usually use z to denote a complex number, a to denote the real part, and b to denote the imaginary part. So, z =  a +  bi, where i=sqrt(-1).  For most purposes, we treat the  For more information about complex numbers, check sosmath.com or sparknotes.com.

Values in the Mandelbrot Set

The Mandelbrot Set consists of all those complex numbers C for which a certain sequence of does not diverge (in other words, the values in the sequence do not get infinitely large). The sequence is a simple one: z_t+1 =  z _t^k +  C, where k=2 and z₀=0+0i. If, after an infinite number of applications of this formula, the magnitude |z | stays small, then the number C is a member of the Mandelbrot Set. Otherwise, C is not a member.

Of course, in practice we cannot apply the formula an infinite number of times, that would take forever! So, instead, we apply the formula a few hundred or a few thousand times, and if |z| stays small for that many repititions, then we assume that it will stay small forever and we call C a member of the set. Here is an example: let's pick two values of C, C1 and C2

          C1 = -0.24148 + 0.66282i
          C2 = -0.23920 + 0.65070i

The table below shows how the magnitude of the z _t values grows as we iterate the formula.
 

	C1	C2
|z0|	0.70544	0.69327
|z2|	0.23788	0.24006
|z4|	0.66476	0.63823
|z6|	0.79042	0.76197
|z8|	0.47733	0.46305
|z10|	0.62832	0.52328
|z12|	1.11106	0.93402
|z14|	1.25657	0.81247
|z16|	2.67593	0.32640
|z18|	52.57986	0.82500

We can see that C₂ looks like it is probably a member of the set, but C₁ definitely is not!

The amazing thing about the Mandelbrot Set is that the boundary between numbers that are members and numbers that are not members is a fractal. No matter how far you zoom in on the boundary, you'll always see more complex wiggles, as shown in the sequence below.

 

Mandelbrot Set Pictures

The computations that go into determining membership in the Mandelbrot Set can be used to draw beautiful pictures.  How can this work?

1. First, select an area of the complex plane.  Usually, you start with an area from about -2-1i to about 1+1i.
2. Divide up this area into individual pixels, based on the height and width of the image you'd like to produce.  Each pixel gets a different complex value C.
3. Select a palette of colors, and a maximum number of iterations you are willing to perform.
4. For each pixel in the image, apply the Mandelbrot formula to the value C. If the point C appears to be in the set, color it black. Otherwise, select a color from your palette of colors based on how many applications of the formula were needed to pass the magnitude value 2.0 (for C₁ above, that would 16).

Surprisingly, the colors of the points that are not in the set form fascinating swirls and spirals and branchings, in many respects far more interesting than the Set itself.

The infinitely fractal nature of the Mandelbrot Set is evident in the patterns we observe around its boundaries.

What is a Julia Set?

A Julia set is a set of points in the complex plane, just like a Mandelbrot set is, but computed with a slightly different approach. Every Julia set is based on a distinct complex seed value C_s. The Julia set for C_s is the set of values z₀ for which magnitude of |z| in the Mandelbrot formula stays small. So, you can see that the Mandelbrot Set and Julia sets are related. However, while there is one unique Mandelbrot Set (for a given power k), there are an infinite number (technical, at least Aleph1) different Julia sets. The picture at right shows the Julia set for the point C_s = -0.13196-0.81295i.

Julia Set Pictures

Like we did for the Mandelbrot Set, you can use the iteration count of a Julia set computation to make a pretty picture. The pictures for a Julia set don't tend to be as fancy as those for the Mandelbrot Set, but they are still very nice. The picture below is the Julia set for C_s = -0.824-0.1711i, colored by how fast the value of the iteration diverges.



There is another way to compute the boundary of a Julia set, by using the inverse computation to derive values of z that could lead to the value C_s. This creates some eerie, spiky pictures. The picture below is the points view of the Julia set at C_s = -0.81-0.1795i.



If you've been paying careful attention, you may have figured out that the Mandelbrot Set essentially serves as a map or index of all the possible Julia sets. Points that are members of the Mandelbrot Set lead to non-empty Julia sets. Points outside the Mandelbrot set can lead to interesting Julia set pictures, but their actual Julia sets are empty.

Image Gallery

Click on the thumbnails on the left to see the image at full size.  All of these images were generated with my Java 2 application JManEx.
 

	This is an image of the full set, slightly zoomed in, using white for the interior color rather than the traditional black.  This image also used a non-linear color mapping to bring out the colors a little more.
	This is an image of a classic 8-pointed star, zoomed in about 50x, near the point -0.415-0.683i.
	This beautiful spiral is shown at a zoom level of about 10000x, but it goes down into infinity.  Spirals like this appear throughout the edges of the Mandelbrot set.  This particular one is near 0.28693186889504513+0.014286693904085048i with a width of about 6.349e-4.
	Miniature almost-copies of the Mandelbrot Set are spread throughout the borderlands of the big set.  Each copy is at least a little different than the full set, and each is joined to the full set by an infinite chain of smaller and smaller additional copies.  This specimen was rendered at a zoom level of about 30,000,000x.
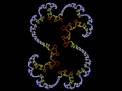
	Whorls and whirlpools appear in many places in the Mandelbrot set, but to find the nicest ones you have to zoom in.  This specimen is near 0.3245046418497685+0.04855101129280834i at a zoom of about 72 million.
	This is a classic curly Julia set, depicted in 'points' mode.  This Julia set corresponds to seed point 0.3245+0.04855i.
	This is a rather blocky-looking Julia set, selected from a bubble off the side of the main Mandelbrot Set, at -0.4961+0.5432i.
	This beautiful Julia set was selected from an interior Mandelbrot Set point very close to the edge, at 0.300283+0.48857i.

Links to Other Mandelbrot/Julia Pages

David Joyce's Mandelbrot/Julia Explorer

A nice interactive web site for generating Mandelbrot and Julia set images.

The FractalZone

Big web site with pictures of all kinds of fractal shapes, including the Mandelbrot Set.

z squared plus c

Very fancy web site with images made from the Mandelbrot Set and a variety of related sets and higher-dimensional analogues.

Christoph Lauer's Mandelbrot Program

Another Java implementation of a Mandelbrot/Julia set program, which shows the Julia set corresponding to a point in or near the Mandelbrot set in real time! (Not an applet, but may be downloaded or started via Java Web Start)

Fractint page

A home site for the most versatile and capable of fractal rendering programs, Fracint. Awesome!