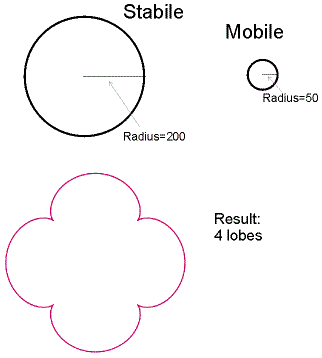
The simplest case is one where the size of the stabile is evenly divisible by the size of the mobile. In this case, the path drawn by the pen simply repeats the same trip around the Stabile every time, as shown in the figure below right.
In the figure shown at right, the radius of the Stabile is 200, and that of the Mobile is 50. Therefore, the perimeter of the Stabile is exactly 4 times that of the Mobile. This combination yields a spirograph figure where the path drawn by the pen has 4 parts or lobes, corresponding to four complete rotations of the Mobile.
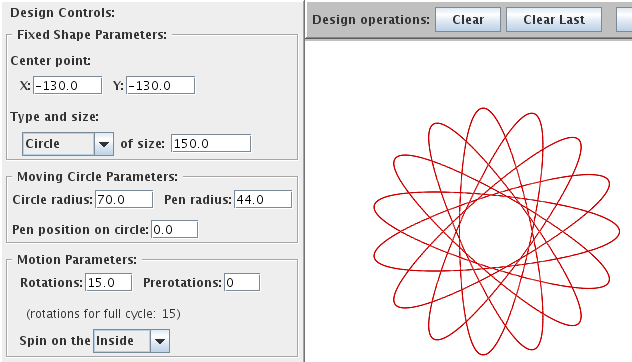
More complicated figures will appear when the size of the Stabile is not an integer multiple of the size of the Mobile. This all falls out of the prime factorization of the sizes. For example, let's say we chose a Stabile size of 150, and a Mobile size of 70. To compute the maximum number of points or lobes that a spirograph drawing will have for those two sizes, we need to divide the Stabile size by the greatest common divisor of the two sizes.
- Stabile size 150 = 2 * 3 * 5 * 5
- Mobile size 70 = 2 * 5 * 7
- Greater common divisor(150,70) = 2 * 5 = 10
- Number of lobes on drawing: 150/10 = 15. (shown below)
If you want a figure with a certain number of rounds N, choose a Stabile size as an integer M * N. Then, choose a Mobile size M * P for some value P, such that M and P are mutually prime. For example, if we wanted a figure with figure with 21 lobes, we would follow the procedure like this:
- Choose a Stabile size 21 * M; let M = 5,
giving Stabile size 105. - Choose a Mobile size 5 * P; let P = 11,
giving a Mobile size of 55.
This kind of design process lets you predictably assemble really nice pictures. Click on the image below to see a two-part drawing that was made with a Stabile size of 105.


