Amazing Spiro Applet Help:
How the Applet Works

This page describes how the spiro applet really works, just in case you were wondering about it. It is divided into three sections.
1. Mechanics of the Spirograph
2. How Spiro draws with dots
3. How Spiro saves your Drawings.

Mechanics of the Spirograph

The Spiro Applet performs a relatively simple simulation of the spirograph mechanics. The mechanics and the math used to support the simulation are described below for each of the applet's two main drawing modes. (Note: in all the diagrams and mathematics below, I'm assuming a coordinate system with the Y axis inverted; this is how most computer windowing systems, including Java AWT, draw.)

Outside Mode   

When the position of the mobile is set to Outside, the mechanics are that of a wheel rolling clockwise along the outside of another wheel (or other shape). The diagram below shows how this work. Note that, in Spiro version 0.98, the pen is always attached to the mobile at the same angle.



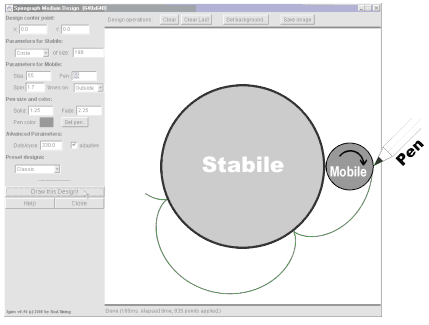
Spiro draws a line by compute a series of position for the pen, by smoothly varying the angular distance travelled by the mobile. Each pen position is computed using the following basic procedure:

• Given the angular distance A in radians rolled by the mobile, and the radius of the mobile R, compute the linear distance L:  L = A * R.
• Using the distance L and the shape and size of the Stabile, compute the normal angle N in radians to the stabile at that distance. How this is computed depends on the shape, but for a circle Stabile of radius RS, it is:  N = L / RS.
• Using the distance L, normal angle N, the design center point (X,Y), and the shape and size of the Stabile, compute the point (CX,CY) where the Mobile and Stabile are in contact. How this is computed depends on the shape, but for a circle Stabile of radius RS, it is:  CX = X + RS * cos(N)    CY = Y + RS * sin(N).
• Using all the previous information, plus the radial distance of the pen from the center of the Mobile D, find the location of the pen (PX,PY) on the Mobile:  PX = CX + R * cos(N) + D * cos(A)     PY = CY + R * sin(N) + D * sin(A).

For a typical drawing, Spiro goes through this procedure about 20000-50000 times, drawing a dot for each location of the pen. When the dots are close enough together, they form a continuous smooth line.

Inside Mode   

When the position of the mobile is set to Inside, the mechanics are that of a wheel rolling counterclockwise along the inside rim of another wheel (or other shape). The diagram below shows how this work. Note that, in Spiro version 0.98, the pen is always attached to the mobile at the same angle.



The mathematics for the Inside mode are very similar to those described for outside.

~Inside Mode

The Spiro applet also supports a third mode of operation, called quasi-inside. This mode does not receive an explanatory diagram, because it doesn't really correspond to any physical system. In fact, the quasi-nside mode was a programming bug that happened to make cool-looking pictures, so it was honored with the status of a special mode.

How Spiro Draws Smooth Lines with Fuzzy Dots

The Java programming language does not have any builtin mechanisms for drawing fancy lines or curves. In general, the best a Java applet can hope for is to draw straight lines with a thickness of one pixel. For the Spiro applet, that was clearly inadequate, so Spiro uses fuzzy-edged dots to do its drawing.

The picture at right shows a close-up of how the dots work. Notice that the dots normally have soft edges, this gives a much smoother look to the line. For a typical drawing, Spiro draws from 6000-60000 individual dots, each of which affects roughly 4-25 pixels of the image.

Two parameters control

How Spiro Saves Your Drawings

Java applets run under some very heavy security restrictions inside your web browser. These security restrictions help protect you from network attacks, but they make it impossible for Java applets to save data directly on your computer. To overcome this problem, the Spiro applet depends on a specially-built system installed at the web server, the CGI Image Reflector.

...more here...