
The paradox of voting is the coexistence of coherent individual valuations and a collectively incoherent choice by majority rule. In an election with three or more alternatives (candidates, motions, etc.) and three or more voters, it may happen that when the alternatives are placed against each other in a series of paired comparisons, no alternative emerges victorious over each of the others: Voting fails to produce a clear-cut winner. (William H. Riker, 1982)The paradox of voting was discovered over 200 years ago by M. Condorcet, a French mathematician, philosopher, economist, and social scientist. However, it received little attention until Duncan Black explained its significance in a series of essays he began in the 1940s. The importance of the voting paradox was not fully realized until several years after Kenneth Arrow published Social Choice and Individual Values in 1951, which contained his General Possibility Theorem. The essence of this theorem is that there is no method of aggregating individual preferences over three or more alternatives that satisfies several conditions of fairness and always produces a logical result. Arrow's precisely defined conditions of fairness and logicality have been the subject of scrutiny by other scholars. However, none have found a way of relaxing one or more of these conditions that results in a generally satisfactory voting system immune from the voting paradox. Thus Arrow's theorem has the profound implication that in many situations there is no fair and logical way of aggregating individual preferences -- there is no way to determine accurately the collective will of the people.
Social choice theorists have invented many vote aggregation systems and have attempted to determine the most appropriate systems for a variety of voting situations. Although there is some agreement about which characteristics are desirable in a vote aggregation system, there is much disagreement as to which characteristics are most important. In addition, the selection is often influenced more by political circumstances than by the advice of theorists. Thus the popularity of a voting system is not necessarily an indication of its fairness.
The choice of a vote aggregation system can influence much more than the results of an election. It can also influence the ability of analysts to interpret election results, and in turn the ability of representatives to understand the wishes of the people they represent and the satisfaction of the electorate that they have had the opportunity to express themselves. This is due to the fact that the various vote aggregation systems require voters to supply varying amounts of information about their preferences and that some systems tend to encourage voters to report their preferences insincerely. In addition, the choice of vote aggregation system could affect the stability of a government, the degree to which an organization embraces or resists change, and the extent to which minorities are represented. It could also affect the ability of the members of an organization to achieve compromise.
This section explores the many types of vote aggregation systems that have been proposed. Throughout this section the term voting system will refer specifically to the vote aggregation component of a voting system. Section 1 introduces criteria with which voting systems may be evaluated. Section 2 discusses majority rule voting and several majoritarian voting methods. Section 3 describes three positional voting methods. Section 4 introduces several multi-stage voting methods which are based on majoritarian and positional methods. Section 5 discusses several types of utilitarian voting methods. Section 6 introduces proportional and semiproportional voting systems, which are positional systems for electing multiple representatives in proportion to their support in the electorate. The vote aggregation systems described in this chapter are summarized in the figure at the end of Section 1.
Voting systems that do not always select the Condorcet winner can be evaluated in terms of their Condorcet efficiency -- the percentage of elections in which the Condorcet winner is selected (assuming there is a Condorcet winner).
Although the Condorcet criterion is a popular means for evaluating voting systems, there are some situations in which it is not clear that the Condorcet winner represents the collective choice. For example, Fishburn presents a scenario in which five voters must choose between five alternatives (a, b, c, d, e). The voters hold the following preference orderings (listed from most preferred to least preferred):

Given this preference profile, a is the Condorcet winner. However, an examination of the number of times each alternative is ranked first, second, etc., bears the following results:
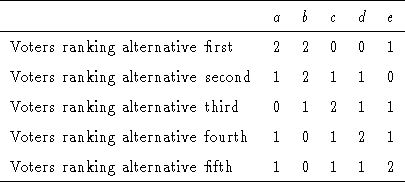
In an examination of rankings, b appears to be the best choice -- with equal first ranks to a and more second and third ranks than a -- yet the Condorcet winner is a.
In cases where the electorate is educated, even the most complicated voting systems are unlikely to pose difficulties for most voters. However, a simple voting procedure may be very important when parts of the electorate are illiterate. In addition, regardless of the literacy of the electorate, any voting system that requires multiple rounds of balloting is likely to be problematic unless the electors are assembled for a meeting.
The advent of high-speed computers diminishes the significance of the number of comparisons necessary to count the votes. Once an important factor for determining the practicality of a voting system, this implementation criterion is now largely irrelevant in most situations where votes are tallied by computer. However, this criterion remains relevant for voting systems in which determining the winner is NP-hard. Another criterion related to system implementation is anonymity. Although most systems can be implemented with secret ballots just as easily as they can be implemented with non-secret ballots, some procedures require action on the part of the voter after initial balloting and thus may be difficult to implement with secret ballots. Cryptographic electronic voting and commerce protocols may provide solutions to this problem.
To understand the first consequence, it is important to realize that it applies to subsets of alternatives. Thus if a group of voters reverse their preference ordering for two alternatives, no change should occur in the outcome with respect to another set of alternatives for which the profiles remain fixed. The same applies to changes in intensity of preferences. Thus voting systems that use cardinal preferences are not independent because a change in intensity of preference for a losing alternative may render it a winning alternative, even if the voters who changed their cardinal preferences do not change their ordinal preferences.
The first consequence of the independence criterion can also be understood by considering Vickrey's definition: "The social choice between any two alternatives shall not be affected by the removal or addition of other alternatives to the field of feasible alternatives under consideration". Arrow gave as an example a situation in which a losing candidate dies after the ballots have been cast. If the voting system is independent, removing that candidate's name (and votes) from the ballots should not change the election winner. If each ballot contains only the name of the voter's most preferred candidate (or an unordered set of preferred candidates), votes for the deceased would be eliminated and the vote totals for the surviving candidates would remain unchanged. However, if the ballots contain an ordinal preference ranking over two or more candidates, those ballots containing votes for the deceased would be recounted with the surviving candidates who are ranked below the deceased bumped up.
The fact that the independence criterion allows voting systems that use minimal information about voter preferences while prohibiting voting systems that take into account more information about voter preferences has made it controversial. Use of this criterion is generally motivated by the fact that it prohibits voting systems that use information that may be considered arbitrary (cardinal preferences) or that tend to promote strategic behavior. However, some theorists argue that in the absence of a perfect voting system, systems that require voters to supply cardinal preferences or ordinal preferences over multiple alternatives should not be ruled out because of a lack of independence. One might also argue that the systems that satisfy the independence criterion do so because they ignore information and essentially waste the votes of all those who do not support one of the top contenders. Thus those who support the "irrelevant" alternatives (those alternatives with little chance of winning) might as well not vote at all. Indeed these systems also promote strategic behavior because they tend to encourage supporters of the irrelevant alternatives to vote for second-choice alternatives with better chances of winning.
The second consequence of the independence criterion is to prohibit voting systems that do not have stable outcomes: that is, voting systems in which a given set of ballots may produce different results each time it is counted. Instability is rarely encountered in the traditional voting systems discussed in the chapter and has not been the subject of much discussion in the literature. It is generally taken for granted that voting systems should not involve random processes, except possibly to to resolve ties. Slaton offers an interesting explanation of this assumption using Newtonian and quantum physics as metaphors. She argues that traditional voting systems stem from a Newtonian world view in which it is believed that the world can be understood through the study of discrete particles whose behavior adheres to strict laws. She contrasts the Newtonian philosophy with the quantum philosophy, which places less emphasis on absolutes and more emphasis on tendencies. Random sampling is thus a reasonable approach to selecting representatives under a quantum world view.
If is a system is not monotonic, a situation may arise in which voters could prevent their favorite alternative from winning by voting for that alternative. Obviously this is contrary to the purposes of a voting system -- voters should not be penalized for supporting their favorite alternative.
Both Pareto-optimality and monotonicity relate to the collective rationality of a group decision-making procedure. Clearly if one were to make a decision based entirely on one's own preferences, one would not select y if one preferred x. The rational individual would select an alternative other than y (x or an alternative preferred to x). Likewise if one had selected x and later received news that x was even better than originally thought or that y was even worse than originally thought, one would not switch the selection to y. The rational individual would stick with the selection of x. When many decision-makers must make a group decision, we can extend the rules we would follow for individual decision-making. Thus if every decision-maker prefers x to y then it would be irrational for the group as a whole to select y. Likewise, if the group selects x and one or more group members decide that x is even better than originally thought or y is even worse than originally thought, the group should not change its decision. Thus with Pareto-optimality and monotonicity, the notion of what is individually rational can be extended easily to what is collectively rational.
Consider the following example. A city council is composed of five representatives, each elected by the voters in a single-member district. Sixty percent of the city's voters are Democrats and 40% are Republicans. The distribution of party membership is fairly even across the five districts. Under this non-proportional representation system, all five representatives elected are Democrats. However, if the five representatives were elected at-large by voters from throughout the city using a proportional representation system, three Democrats and two Republicans would be elected.
Related to proportionality is the average ballot effectiveness. The effectiveness of an individual ballot may be defined as the proportion of a ballot that is used to vote for a candidate that ends up winning. In elections where each voter votes for one candidate and the candidate with the most votes wins, all ballots voting for the winning candidate are 100% effective while the remaining ballots are 0% effective. The more proportional a voting system, the greater its average effectiveness is likely to be.
Nurmi evaluates voting systems' tendencies to encourage manipulation in terms of the information required for successful manipulation. He sketches a four-level hierarchy for preference misrepresentation. At the first level of the hierarchy are those systems that require knowledge of only the "distribution of first preferences over alternatives" in order to be manipulated. At the second level are those systems that require knowledge of "distribution of approval over alternatives". At the third level are those systems that require knowledge of the "binary comparison matrix". And at the fourth and most difficult to manipulate level are those systems that require knowledge of the "entire preference profile".
While Nurmi's hierarchy is helpful in identifying the relative difficulties involved in obtaining the information necessary to manipulate an election, it does not distinguish voting systems based on the ease with which this information may be applied or the chances that this information will reveal preference profiles over which manipulation is possible. Indeed, it has been shown that manipulating some voting systems is an NP-hard problem, even with perfect information about voter preference profiles. Nurmi's hierarchy also fails to distinguish between systems manipulated most successfully by individuals (micromanipulation) and those manipulated most successfully by coalitions (coordinated macromanipulation).
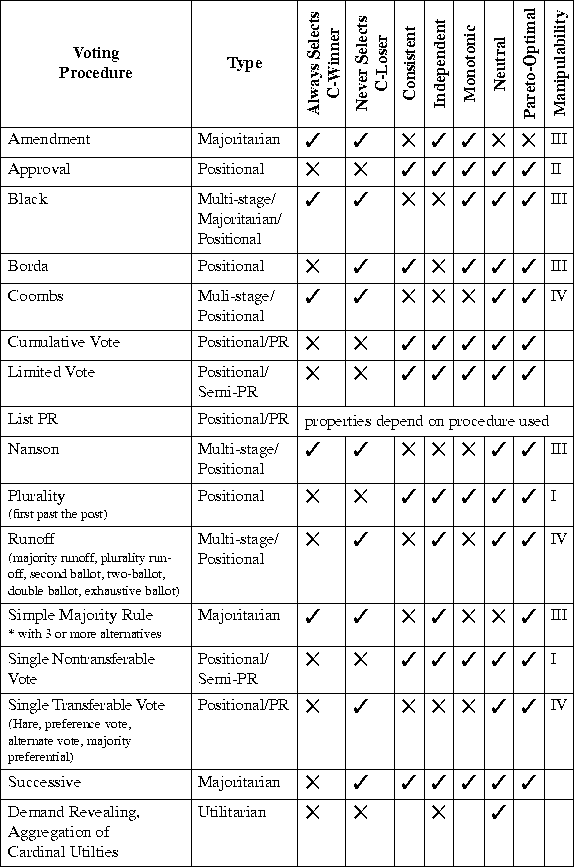
Figure: Properties of vote-aggregation procedures. Check marks
indicate properties possessed by the voting system in that row, Xs indicate
properties not possessed by the voting system in that row. Cells have been
left blank where information is unavailable or varies depending on the
specific details of the procedure used.
Unfortunately, decisions can rarely be considered as a choice between two alternatives unless another mechanism has been used to eliminate all but two alternatives or divide the alternatives into two groups. The two-party system in the United States serves to narrow down the fields of candidates so that only two candidates compete for each office in most state and national elections. Parliamentary procedures generally involve an amendment protocol that results in all votes being binary choices between a new proposal and the status quo or a proposal and an amendment. But when runoff elections or amendment procedures are used to reduce the field of alternatives to two, alternatives may be eliminated that could actually win the election if an alternate procedure were used. Thus when majority rule is used with three or more alternatives, one or more criteria may be violated as a result of the procedure used to narrow down the alternatives. For example, Riker presents a scenario in which monotonicity is violated when 13 voters choose between four alternatives (w, x, y, z). The voters hold the following preference orderings:

In a one-person-one-vote election, w receives four votes, x receives four votes, y receives three votes, and z receives two votes. If all but the top two alternatives are eliminated, w and x will compete in a simple majority runoff election. In this election voters 9 through 13 will each vote for their second choice, as their first choices have been eliminated. Thus w will receive six votes and x will receive seven votes. Now, suppose voters 1 and 2 change their minds and decide to reverse their preferences for x and w -- increasing the overall support for x. In this case the runoff election will be a contest between x and y. Given that the support for x has increased, we might expect x to remain victorious. However, in this case y beats x seven votes to six. Thus the runoff procedure has caused monotonicity to be violated.
Simple majority rule may be applied to three or more alternatives by comparing the alternatives two at a time, eliminating an alternative if it loses a pairwise comparison. However, the order in which alternatives are selected for comparison may determine the outcome of the election. For example, given the above preferences, either w, x, or y might win, depending on what order they are selected for comparison.
Majoritarian methods extend the principles of majority rule for more than two alternatives by selecting the alternative that can beat all other alternatives in pairwise comparisons (the Condorcet winner). However, such an alternative is often non-existent, and these methods must provide additional procedures for selecting a winner in the absence of a Condorcet winner. Because these methods rely on binary comparisons between all candidates, voters must supply their complete preference orderings or the election must be conducted with multiple rounds of balloting. Thus, knowledge of the binary comparison matrix is required for them to be manipulated.
Many majoritarian methods have been proposed, most of which are monotonic and result in the selection of the Condorcet winner when one exists. All violate the consistency criterion, and they have differing outcomes in the absence of a Condorcet winner. Except for the amendment procedure, these methods are rarely used. The following examples of majoritarian methods are described by Riker and Nurmi.
The Schwartz rule selects the set of alternatives over which the collective preferences are cyclic and the entire cycle is preferred over the other alternatives. When there is a Condorcet winner it is the single element in such a set. However, in the absence of a Condorcet winner most or all of the alternatives may be members of this set. The Schwartz rule is not Pareto-optimal.
Other majoritarian procedures include the maximin method, Dodgson's method, and the Kemeny rule. Determining the winner using Dodgson's and Kemeny's procedures is NP-hard.
Unlike majoritarian methods, which use only information from binary
comparisons between candidates, positional methods take into account information
about individuals' preference orderings. However, these methods do not
necessarily take into account a voter's entire preference ordering. In
this section, three single-stage positional methods are described: plurality
voting, which uses only information about each voter's most preferred alternative;
approval voting, which uses information about a varying number of top alternatives
for each voter; and the Borda count, which uses information about each
voter's entire preference ordering. These methods do not necessarily select
the Condorcet winner when one exists. In addition, for some sets of voter
preference profiles, each method produces a different outcome. The three
positional methods described here are all monotonic and Pareto-optimal.
In plurality elections with three candidates, two candidates with somewhat similar ideological views will sometimes both lose to a candidate with opposite views. However, after the election the supporters of the two losing candidates may realize that had they worked together and supported a single candidate, that candidate could have won easily. In the next election, these supporters are more likely to compromise and back a single candidate. Thus, over time, plurality voting encourages parties to offer only two candidates -- reducing plurality voting to simple majority rule. Plurality voting is widely used for governmental elections in the United States and has been credited with helping to maintain the two-party system.
Plurality voting is classified at the first level of Nurmi's preference misrepresentation hierarchy and is generally considered to be one of the easiest voting systems to manipulate.
Approval voting is currently used by several professional societies, including the Institute of Electrical and Electronics Engineers, the Mathematical Association of America, the American Statistical Association, and The Institute of Management Sciences. It tends to promote the election of moderate candidates and prevent situations in which the candidate elected is ranked last by those who did not vote for him or her. It also tends to encourage three or more alternatives to be considered in an election. If all voters approve of only their first choice alternatives, approval voting results in the same outcome as plurality voting.
Nurmi classifies approval voting at the second level of his preference misrepresentation hierarchy because it requires knowledge of the distribution of approvals over alternatives in order to be manipulated. In addition, Brams and Fishburn assert that approval voting is less likely to be manipulated than plurality voting because it presents voters with fewer situations in which it is advantageous to vote strategically. In many situations where plurality voters would fare better by voting for a second choice, approval voters can maximize their voting power by voting for both their first and second choices.
As with plurality voting, approval voting does not necessarily select the Condorcet winner when one exists. However, approval voting has a higher Condorcet efficiency than plurality voting, selecting the Condorcet winner in all cases where it is selected by plurality voting as well as in other cases where it it may not be selected by plurality voting.
This system, as well as other similar 'scoring' or 'point' methods, incorporate all voter preference information into the vote aggregation. However, as with the other positional voting methods, this does not always produce a logical result. In fact, the result of a Borda count election is often a function of the number of alternatives considered. However, the Borda count will never choose the Condorcet loser.
The Borda count is one of the few single-stage voting methods that fails to satisfy the independence of irrelevant alternatives criterion. This failure may be observed, for example, in a three-alternative election when two alternatives are tied for first place. If one voter switches his or her preference ordering for one of the tied alternatives and the third alternative without switching his or her preference ordering for the tied alternatives, the tie may be broken. For the irrelevance of independent alternatives criterion to hold, a switch in preference ordering not involving the tie should not affect the tie.
Although the Borda count was initially criticized for its susceptibility to manipulation (before it was known that all non-dictatorial voting systems with at least three possible outcomes are manipulable) later analysts have found it to be a mixed bag. Saari showed that the Borda count is less susceptible to micromanipulation than many other voting systems while Chamberlin demonstrated that the Borda count is more susceptible to coordinated macromanipulation than plurality rule and other positional voting systems. Nurmi places the Borda count and its variations (including its multi-stage variations) at the third level of his hierarchy, noting that although voters submit their entire preference profiles, only binary comparisons are necessary to determine the election result and thus the binary comparison matrix is all the information needed to manipulate the election.
Multi-stage procedures use either different choice functions at
different stages of the procedure, or one choice function iteratively on
diminishing sets of alternatives. The following methods are representative
of the multi-stage procedures that have been proposed. All of these methods
are Pareto-optimal. In addition, they have the advantage that voters can
often vote for a preferred candidate who has little chance of winning without
"wasting" an opportunity to vote for a more viable second-choice candidate
(of course situations still arise where it is in a voter's best interest
to vote insincerely). Thus voters are likely to have fewer incentives to
vote insincerely with multi-stage procedures than with single-stage procedures.
Nurmi considers this procedure relatively difficult to manipulate and classifies it at the fourth level of his preference misrepresentation hierarchy. However, the fact that it is not monotonic indicates that when voters have the necessary information, they will find opportunities for manipulation frequently.
A variation of this procedure used to elect the French National Assembly eliminates all candidates who do not receive a specified threshold of votes on the first ballot. As the second ballot may contain more than two candidates, the winner is the one who receives a plurality of votes.
Another variation on this procedure is the exhaustive ballot procedure in which the alternatives with the least votes are eliminated one at a time in a series of elections. This procedure can be time consuming and result in decreasing voter participation with each round of balloting.
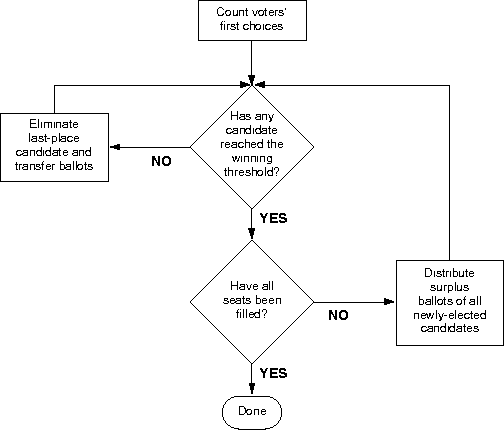
Figure: Procedure for counting votes in a single transferable
vote election
There are many variations on this procedure with different methods for calculating the quota needed for election, different redistribution procedures, and different methods for resolving ties. The procedure used to elect the Cambridge City Council and School Committee uses the Droop threshold to determine the quota needed for election. Any candidate receiving votes greater than the total number of votes divided by one more than the number of seats to be filled is elected. In Cambridge elections, votes are redistributed through a method of controlled randomness. For example if a candidate x receives 5000 votes and it is determined that only 4000 votes are needed to pass the Droop threshold, 1000 excess votes must be redistributed. The ballots for x are numbered and every fifth one is redistributed. (In Cambridge, ballots in each precinct are sorted according to the first choice listed. The piles of ballots for each precinct are merged according to a randomly determined precinct order.) While it is theoretically possible for this method to result in different election outcomes depending on the way the ballots happen to be ordered (due to second- or lower-choice alternatives being unevenly distributed among the ballots), a study by the Center for Voting and Democracy indicates that such outcomes are probably rare. The possibility of differing outcomes can be eliminated completely through the use of a mathematical redistribution system. In this system the excess ballots for candidate x in the above example would be distributed by redistributing one fifth of every ballot cast for x to the second choice indicated on that ballot. This method extends considerably the amount of time necessary for vote counting when ballots are tallied by hand. However, computerized vote-counting systems make mathematical redistribution practical.
The use of STV generally results in elections with high average effectiveness because all ballots that can be used to elect a candidate, either as a first-choice or on a transfer, have some degree of effectiveness. Because STV allows for redistribution of surplus votes when multiple candidates are to be elected, a single vote may be effective in helping elect more than one candidate.
Some theorists have criticized STV for its violation of several normative criteria. If the Condorcet winner is not eliminated in an STV election, it will be selected; however, it is possible for the Condorcet winner to be eliminated. Furthermore, this procedure is not monotonic and thus may result in perverse outcomes in which a candidate would be better off with fewer votes. In practice it is extremely difficult to detect violations of monotonicity in STV elections and thus such violations are rarely exploited or challenged.
STV requires knowledge of the entire preference profile to be manipulated and thus falls in the fourth level of Nurmi's hierarchy. In addition, to the typical form of manipulation in which voters misrepresent their preference orderings, STV is also vulnerable to manipulation in which voters truncate their preference list and do not reveal their complete preference orderings. Despite the fact that examples of such vulnerability have been provided by Brams and Fishburn, literature explaining STV to voters continues to deny that truncation of preferences is ever advantageous. This denial is probably of little consequence, however; as situations in which truncation or any other form of manipulation are advantageous in an STV election are almost impossible to detect. But as Dummett explains, situations may arise in which parties may be able to coordinate successful macromanipulation. He proposes an example in which STV is used to select one of three candidates, a, b, or c:
With detailed and reasonably accurate information about the intentions of the voters, such as can be obtained from well-conducted opinion polls, and with a thorough canvass to identify its own supporters, an organized group such as a political party can...instruct sufficiently many supporters to list a highest to ensure that a is not eliminated at stage 1, and instruct the rest to list b highest, in order to bring about the elimination of a's principal rival c.STV is most vulnerable to such manipulation when it is used for elections in which one candidate is to be selected from a small pool of candidates. When multiple candidates are to be selected or when the pool of candidates is large, obtaining complete preference profiles for all voters and doing the computations necessary to find opportunities for manipulation is likely to be quite difficult.
This procedure is not monotonic and does not always chose the Condorcet winner when one exists. However, it will not select the Condorcet loser. While STV tends to select the most intensely preferred alternative, Coomb's procedure tends to select the alternative viewed as least intolerable by the majority. It requires knowledge of the entire preference profile to be manipulated and thus falls in the fourth-level of Nurmi's hierarchy.
Utilitarian voting methods require voters to assign utility
values to each alternative. Utility values can be thought of as measures
of expected happiness with each alternative on some finite scale. These
utilities are aggregated to determine the election outcome. Riker explains
the rationale behind these methods:
Majoritarian methods base decision on how many times x is ahead of one other alternative. Positional methods base decision on how many times x is ahead of all other alternatives. Neither bases decision on voters' direct valuation of alternatives, although positional methods are sometimes mistakenly so interpreted. Many writers, however, have argued that the intensity of judgment or direct valuation ought to be incorporated into the decision. The voting method should reveal not only that x is ahead of y, but by how much.These methods do not necessarily select the Condorcet winner when one exists. They also violate the independence of irrelevant alternatives criterion. These methods do not fit cleanly into Nurmi's preference misrepresentation hierarchy because voters are likely to misrepresent the intensity of their preferences using these methods, even if they do not misrepresent their preference orderings. In order to manipulate the election successfully by misrepresenting their preference orderings, voters would need to know not only the entire ordinal preference profile required for Nurmi's fourth level systems, but also information from the cardinal preference profile. However, manipulation may be possible through misrepresentation of preference intensity without any additional information.
Several types of utilitarian methods described by Riker and Mueller are introduced below.
Riker criticizes this system for promoting inequality by providing an advantage to those whose budgets will be least impacted by paying a tax. He also criticizes it for encouraging coercion in an attempt to minimize the tax. However, Tullock notes that the system need not use real money. Each citizen might be given a certain number of points which he or she may use for paying the voting taxes. He does not comment on the possibility of markets developing for buying and selling these points. In addition, Riker notes that this system cannot be used in secret-ballot elections because it requires public revelation of individual offers in order to assess the taxes. However, cryptographic electronic voting and payment systems might make such a system practical without public revelation of offers.
Proportional representation (PR) and semiproportional representation
systems are designed to promote close correspondence between the proportion
of supporters of each party (or other interest group) in the electorate
and the proportion of seats held by each party in a governing body. To
achieve this goal, these systems require the electorate to be divided into
constituencies such that each elects more than one representative. There
is a wide variety of methods used to achieve proportional representation,
and each succeeds to varying degrees. Although on average PR systems produce
results more proportional than produced by plurality voting systems, some
PR systems are in reality less proportional than most plurality systems.
Several countries have recently adopted mixed-member proportional representation
systems (MMP) in which some representatives are elected from single-member
districts and others are elected at-large using a PR system.
Proportional representation was introduced in the nineteenth century as a way to provide representation for interests that could not be represented when a single representative was elected from each geographic community. After the breakup of the European empires at the beginning of the twentieth century, PR was selected by many countries in order to ensure that the educated minority would be represented in the new governments.
The many varieties of proportional representation systems that have been used to elect legislatures around the world can be divided into two categories: list PR (which employs a variation on plurality rule) and single transferable vote. The semiproportional systems all employ a variation on plurality rule. Although the goal of proportional representation might be pursued through adaptations of any of the positional or majoritarian voting methods, only plurality rule and STV have been used in practice.
In the simplest case, the entire country is treated as a single constituency, and the legislative seats are allocated in exact proportion to the support for each party among the electorate. However, even in this simple case, the mathematics of the situation may preclude the achievement of perfect proportionality. A country of population P represented by L legislators would ideally select one representative for each P/L voters. But it is unlikely that the vote totals for each party will be exact multiples of P/L, and fractional representatives are not an option. Several methods have been developed to solve this problem both in the case of a single constituency country and in the more usual case where a country is divided into many constituencies.
One of the easiest ways to allocate seats is to establish a quota necessary to win each seat. In this largest remainder method the parties are first allocated one seat for each multiple of the quota they have received. All votes received beyond an even multiple of the quota are a remainder. The remaining seats are allocated to the parties with the largest remainders. There are also more complicated methods, such as the largest average rule, that tend to have more proportional results.
The methods used to determine which individual will fill each seat vary in the extent to which they emphasize the influence of parties versus the opinions of individuals. The simplest forms leave the decision entirely up to the party while more complicated systems respect voters' opinions to varying degrees.
In the basic list systems, the parties prepare lists that include as many candidates as there are seats to be filled. The voters select the list for the party they support and deposit it in their ballot envelopes. After the votes are counted and the seats are allocated, each party selects from the top of its list the number of candidates corresponding to the number of seats won. A party winning one seat would select the candidate at the top of its list, a party winning two seats would select the top two candidates, and so on. The candidate at the bottom of the list has almost no chance of being elected.
Some countries allow voters to vote either for a party list or for a particular candidate on the list. In Belgium, for example, the vote tallies are added up for all of the candidates who received individual votes. All that receive enough votes to meet the quota are elected. The votes for the party list are then divided among the candidates on that list as follows: The first candidate on the list takes as many votes from the party list pool as are needed to meet the quota. If any votes remain in the pool the next candidate on the list takes as many as are needed to meet the quota, and so on until there are no more votes left in the pool. The more voters who choose to vote for the party list, the more influence the party has on the election result. In practice, the percentage of voters who do not vote for the party list (or take advantage of election laws in some countries that let them cross out candidates on their party list) is generally small.